"When you go too far up, abstraction-wise, you run out of oxygen. Sometimes smart thinkers just don't know where to stop, and they create this absurd, all-encompassing, high-level pictures of the universe that are all good and fine, but don't actually mean anything at all. These are the people I call Architecture Astronauts"
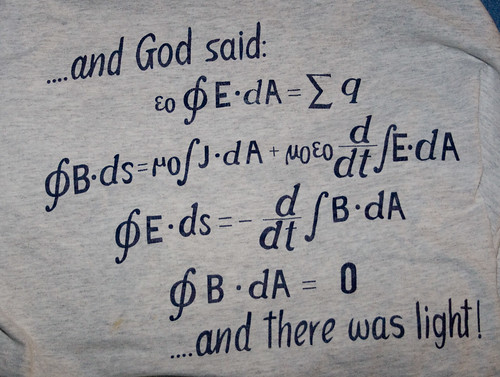 Joel Spolsky en Joel on Software
Joel Spolsky en Joel on SoftwareTraducción casera: "Cuando vas demasiado lejos, en términos de abstracción, te quedas sin oxígeno. En ocasiones, los "pensadores" simplemente no saben dónde parar y crean estas absurdas y globales teorías de alto nivel sobre el universo que son buenas y depuradas, pero que en realidad no significan absolutamente nada. Estos son la gente que yo llamo Astronautas de la Arquitectura".
A veces los científicos vamos más allá de la realidad y nos olvidamos de que lo que tratamos de hacer es simplemente representar la realidad. Los árboles en muchas ocasiones no nos dejan ver el bosque.
Esta reflexión ha venido esta semana a mi mente después de haber asistido a un curso sobre Computational Fluid Dynamics (CFD). Para aquellos que no estén familiarizados con el término (pienso que el 99,9999 % de los mortales...) os resumiré la idea. Se trata de simular (predecir) mediante ecuaciones el movimiento de fluidos (líquidos o gases) cuando se encuentran con diferentes obstáculos. Estos obstáculos pueden ser otros fluidos o sólidos. El ejemplo más "terrestre" que puedo encontrar es el trabajo en túneles del viento que llevan a cabo los equipos de Fórmula 1.
Pues bien, según el especialista que nos impartió el curso, uno de los principales problemas del CFD es verificar los resultados de los modelos utilizados ya que es muy difícil hacer medidas experimentales. Sin embargo, ni corto ni perezoso, también dijo que muy probablemente los resultados de las simulaciones fuesen más precisos que los experimentos. Es decir, la ficción supera a la realidad.
¿Cómo puede ser que las ecuaciones de un modelo que es inherentemente una aproximación de la realidad sean de una mayor confianza que la propia realidad? ¿Y si el modelo no es el adecuado? ¿Y si las ecuaciones que hasta ahora se han considerado como válidas, en un futuro se demuestra que son incorrectas? Entonces, tendremos que tirar a la basura el verdadero objeto de todas estas investigaciones: los miles de artículos publicados en revistas científicas de primer nivel.
Fotografía | Maxwell's Equations de DJOtaku
A veces los científicos vamos más allá de la realidad y nos olvidamos de que lo que tratamos de hacer es simplemente representar la realidad. Los árboles en muchas ocasiones no nos dejan ver el bosque.
Esta reflexión ha venido esta semana a mi mente después de haber asistido a un curso sobre Computational Fluid Dynamics (CFD). Para aquellos que no estén familiarizados con el término (pienso que el 99,9999 % de los mortales...) os resumiré la idea. Se trata de simular (predecir) mediante ecuaciones el movimiento de fluidos (líquidos o gases) cuando se encuentran con diferentes obstáculos. Estos obstáculos pueden ser otros fluidos o sólidos. El ejemplo más "terrestre" que puedo encontrar es el trabajo en túneles del viento que llevan a cabo los equipos de Fórmula 1.
Pues bien, según el especialista que nos impartió el curso, uno de los principales problemas del CFD es verificar los resultados de los modelos utilizados ya que es muy difícil hacer medidas experimentales. Sin embargo, ni corto ni perezoso, también dijo que muy probablemente los resultados de las simulaciones fuesen más precisos que los experimentos. Es decir, la ficción supera a la realidad.
¿Cómo puede ser que las ecuaciones de un modelo que es inherentemente una aproximación de la realidad sean de una mayor confianza que la propia realidad? ¿Y si el modelo no es el adecuado? ¿Y si las ecuaciones que hasta ahora se han considerado como válidas, en un futuro se demuestra que son incorrectas? Entonces, tendremos que tirar a la basura el verdadero objeto de todas estas investigaciones: los miles de artículos publicados en revistas científicas de primer nivel.
Fotografía | Maxwell's Equations de DJOtaku







